Rotary Device Sizing Tool

Rotary Device Sizing Tool

Table shape and dimensions

Drive shaft dimension

Load shape and dimensions

Table support (Leave the fields blank if the friction coefficient can be ignored)

Free Shipping for Online Orders. Terms and conditions apply.

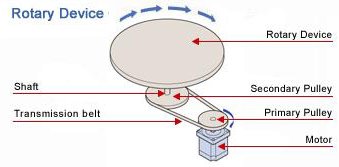
Rotary Device

Unit
Select the unit	Imperial Metric

Round Table

Rectangular table

Table diameter

D = in mm

A = in mm

B = in mm

Table weight mass

W m = lb kg

If you are not sure about the weight mass

Table thickness

t = in mm

Table Material

ρ =

Shaft diameter

D₂ = in mm

Shaft weight mass

W₂ m₂ = lb kg

If you are not sure about the weight mass

Length

L = in mm

Material

ρ₂ =

No additional load	Cylinder type	Rectangular pillar type

Load diameter

D₁ = in mm

A₁ = in mm

B₁ = in mm

Distance from the table center to the load center

Distance

r = in mm

Number of loads

n = pc

Weight Mass of load

W₁ m₁ = lb/pc kg/pc

If you are not sure about the weight mass

Load height

h₁ = in mm

Load material

ρ₁ =

= ( J_L / 386 ) ( V_m / ( 9.55 × t₁ )) ( 1 / 16 )

= ( / 386 ) × ( / ( 9.55 × )) × ( 1 / 16 )

= [lb·in] [N·m]

Friction coefficient between the table and the supporting mechanism

μ=

Distance from the table center to the supporting mechanism
(Please specify the diameter if you use Ball bearing)

Ball Bearing

l = in mm

System efficiency

η= %

Transmission belt and pulleys or gears (Leave the fields blank if a direct coupling structure is used)
Primary pulley (gear) pitch circle diameter (PCD) or diameter		Secondary pulley (gear) pitch circle diameter (PCD) or diameter
D_p1	= in mm	D_p2	= in mm
Primary pulley (gear) weight mass		Secondary pulley (gear) weight mass
W_p1 m_p1	= lb kg	W_p2 m_p2	= lb kg

*If you are not sure about the weight mass*		If you are not sure about the weight mass
Primary pulley (gear) thickness		Secondary pulley (gear) thickness
L_p1	= in mm	L_p2	= in mm
Primary pulley (gear) material		Secondary pulley (gear) material
ρ_p1	=	ρ_p2	=

Mechanism condition
Horizontal operation	Vertical operation

Other requirement(s)
	It is necessary to hold the load even after the power supply is turned off. → You need an electromagnetic brake.
	It is necessary to hold the load after the motor is stopped, but not necessary to hold after the power supply is turned off.

Operating conditions

Fixed speed operation	Operating speed	V₁	=	r/min
	Acceleration/Deceleration	t₁	=	s

Variable speed operation	Operating speed	V₁	=	r/min	〜	V₂	=	r/min
	Acceleration/Deceleration	t₁	=	s

Positioning operation (Fill in the fields, if any)
	Rotor inertia	J_O	=	oz·in kg·m ²
	Gear ratio	i	=
	If the rotor inertia and the gear ratio are unknown, the acceleration torque will be calculated with an inertia ratio of 5:1 (see the motor selection tips that will appear on the result window for the detail).
	Positioning distance	θ	=	°
	Positioning time	t₀	=	s	Stopping time	t_s	=	s
	If a specific acceleration / deceleration time is required	t₁	=	s
	If a specific operating speed is required	V	=	r/min
If Positioning distance is given and acceleration/deceleration is unknown, it is calculated as one fourth of Positioning time.

Stopping accuracy
Stopping accuracy	±	Δθ	=	°	or
Stopping accuracy	±	Δl	=	in mm	Load center circumference Table circumference

Safety factor
Safety factor

The following is the estimated requirements. Please contact 1-800-468-3982 ( from overseas 1-847-871-5931 ) for assistance or questions.


Load Inertia	J_L	= [oz·in [kg·m ²]
Required Speed	V₁	= [r/min]
	V₂	= [r/min]
Required Torque	T	= [lb·in] = [oz·in] [N·m]
RMS Torque	T_rms	= [lb·in] = [oz·in] [N·m]
Acceleration Torque	T_a	= [lb·in] = [oz·in] [N·m]
Load Torque	T_L	= [lb·in] = [oz·in] [N·m]
Required Stopping Accuracy	Δθ	= [deg]
Other Requirement(s)

To print the calculation report, click Full Report
To view the motor selection tips, click Tips

Call 1-800-GO-VEXTA(468-3982) or 1-847-871-5931

- given information -

Table shape and dimensions
	Table type		=
	Diameter		D = [in] [mm]
	Width		A = [in] [mm]
	Depth		B = [in] [mm]
	Weight Mass		W m = [lb] [kg]
	Thickness		t = [in] [mm]
	Material		ρ = [oz/in [kg/m ³]

Drive shaft dimension
	Shaft diameter		D₂ = [in] [mm]
	Shaft weight mass		W₂ m₂ = [lb] [kg]
	Shaft length		L = [in] [mm]
	Shaft material		ρ₂ = [oz/in [kg/m ³]

Load shape and dimensions
	Load type
	Diameter		D₁ = [in] [mm]
	Width		A₁ = [in] [mm]
	Depth		B₁ = [in] [mm]
	Distance from the table center to the load center		r = [in] [mm]
	Number of loads		n = pc
	Load weight mass		W₁ m₁ = [lb] [kg]
	Load height		h₁ = [in] [mm]
	Load material		ρ₁ = [oz/in [kg/m ³]

Table support
	Friction coefficient between the table and the supporting mechanism		μ =
	Distance from the table center to the supporting mechanism		l = [in] [mm]
	System efficiency		η = %


	Primary pulley (gear)		Secondary pulley (gear)
pitch circle diameter (PCD)	D_p1	= [in] [mm]	D_p2	= [in] [mm]
weight mass	W_p1 m_p1	= [lb] [kg]	W_p2 m_p2	= [lb] [kg]
thickness	L_p1	= [in] [mm]	L_p2	= [in] [mm]
material	ρ_p1	= [oz/in [kg/m ³]	ρ_p2	= [oz/in [kg/m ³]

Mechanism Condition
	Mechanism Condition

Other requirement(s)
	Is it necessary to hold the load even after the power supply is turned off?	→
	Is it necessary to hold the load after the motor is stopped, but not necessary to hold after the power supply is turned off?	→


Fixed speed operation	Operating speed	V₁	=	[r/min]
	Acceleration / deceleration time	t₁	=	[s]


Variable speed operation	Operating speed	V₁	=	[r/min]
		V₂	=	[r/min]
	Acceleration / deceleration time	t₁	=	[s]


Positioning operation	Rotor inertia	J_O	=	[oz·in kg·m ²]
	Gear ratio	i	=
	Positioning distance	θ	=	°
	Positioning time	t₀	=	[s]
	Stopping time	t_s	=	[s]
	Acceleration / deceleration time	t₁	=	[s]
	Specified speed	V	=	[r/min]


Stopping accuracy	± Δθ	= °
	± Δl	= [in] [mm]

Safety factor
	Safety factor	S·F	=

- calculated result -


J_t	= (1/8) (w × 16 ) × D² (π/32) ρ t × D⁴ (1/12) (w × 16) (A² + B²) (1/12) p A B t (A² + B²) (1/8) m × (D × 10^-3)² (π/32) ρ (t × 10^-3 ) × (D × 10^-3)⁴ (1/12) m ( (A × 10^-3)² + (B × 10^-3)²) (1/12) ρ (A × 10^-3) (B × 10^-3) (t × 10^-3 ) ( (A × 10^-3 )² + (B × 10^-3 )²)
	= (1/8) ( × 16 ) × ² (3.4/32) × × ⁴ (1/12) ( × 16 ) × ( ² + ² ) (1/12) × × × × ( ² + ² ) (1/8) × × ( × 10^-3)² (3.4/32) × ( × 10^-3) × ( × 10^-3)⁴ (1/12) × ((× 10^-3)² + (× 10^-3)² ) (1/12) × × ( × 10^-3) × ( × 10^-3) × ( × 10^-3) (( × 10^-3)² + ( × 10^-3)² )	= [oz·in [kg·m ²]
J_S	= (π/32) ρ₂ L D₂⁴ (1/8) (W₂ × 16) × D₂² (π/32) ρ (L × 10^-3) (D₂ × 10^-3)⁴ (1/8) m₂ (D₂ × 10^-3)²
	= ( 3.14 / 32 ) × × × ⁴ (1/8) × ( × 16 ) × ² = ( 3.14 / 32 ) × × ( × 10^-3) × ( × 10^-3)⁴ (1/8) × × ( × 10^-3)²	= [oz·in [kg·m ²]
J₁	= ((1/8) (W₁ × 16) × D₁² + (W₁ × 16) r²) × n ((π/32) ρ h₁ D₁⁴ + (π/4) ρ h₁ D₁² r²) × n (1/12) (W₁ × 16) × (A₁² + B₁² + 12 × r²) × n (1/12) (ρ A₁ B₁ h₁ (A₁² + B₁² + 12 × r²) × n ((1/8) m₁( D₁ ×10^-3)² + m₁ (r ×10^-3)²) × n ((π/32) ρ (h₁ ×10^-3) (D₁ ×10^-3)⁴ + (π/4) ρ (h₁ ×10^-3) (D₁ ×10^-3)² (r ×10^-3)² ) × n (1/12) m₁ ((A₁ ×10^-3)² + (B₁ ×10^-3)² + 12 × (r ×10^-3)²) × n (1/12) ρ (A₁ ×10^-3) (B₁ ×10^-3) (h₁ ×10^-3) ((A₁ ×10^-3)² + (B₁ ×10^-3)² + 12 × (r ×10^-3)²) × n
	= ((1/8) × ( × 16) × ² + ( × 16) × ²) × ((3.14/32) × × × ⁴ + (3.14/4) × × ² × ²) × (1/12) ( × 16) × ( ² + × ² + 12 × ²) × (1/12) ( × × × ) × ( ² + ² + 12 × ²) × ((1/8) × × ( ×10^-3)² + ( × 16) × ( ×10^-3)²) × ((3.14/32) × × ( ×10^-3) × ( ×10^-3)⁴ + (3.14/4) × ( ×10^-3) × ( ×10^-3)² × ( ×10^-3)²) × (1/12) × × (( ×10^-3)² + × ( ×10^-3)² + 12 × ( ×10^-3)²) × (1/12) × × ( ×10^-3) × ( ×10^-3) × ( ×10^-3) × (( ×10^-3)² + ( ×10^-3)² + 12 × ( ×10^-3)²) ×	= [oz·in [kg·m ²]
J_Dp1	= ( 1 / 8 ) w_p1 × 16 × D_p1 m_p1 × (D_p1×10^-3) ²
	= ( 1 / 8 ) × × 16 × ( ×10^-3) ²	= [oz·in [kg·m ²]
J_Dp1	= ( π / 32 ) ρ_p1 ( L_p1 ×10^-3) ( D_p1 ×10^-3) ⁴
	= ( 3.14 / 32 ) × × ( ×10^-3) × ( ×10^-3) ⁴	= [oz·in [kg·m ²]
J_Dp2	= ( 1 / 8 ) w_p2 × 16 × D_p2 m_P2 × (D_P2×10^-3) ²
	= ( 1 / 8 ) × × 16 × ( ×10^-3) ²	= [oz·in [kg·m ²]
J_Dp2	= ( π / 32 ) ρ_p2 ( L_p2 ×10^-3) ( D_p2 ×10^-3) ⁴
	= ( 3.14 / 32 ) × × ( ×10^-3) × ( ×10^-3) ⁴	= [oz·in [kg·m ²]
J_L	= ( J_t + J_s + J_l + J_Dp2 ) ( D_p1 / D_p2 )² + J_Dp1
	= ( + + + ) × ( / )² +	= [oz·in [kg·m ²]
J_L	= J_t + J_s + J_l
	= ( + + )	= [oz·in [kg·m ²]

Required Speed

	V_m	= V ( D_p2 / D_p1 )
		= × ( / )	= [r/min]

V_m1	= V₁ ( D_p2 / D_p1 )
	= × ( / )	= [r/min]
V_m2	= V₂ ( D_p2 / D_p1 )
	= × ( / )	= [r/min]

V_m	= V × ( D_p2 / D_p1 )
	= × ( / )	= [r/min]
V_m	( θ / 360) × ( 60 / ( t₀ - t₁ ) ) × ( D_p2 / D_p1 )
	( / 360) ) × (60 / ( - )) × ( / )	= [r/min]


T	= ( T_a + T_L ) ( Safety Factor )
	= ( + ) ×	= [lb·in] [N·m]
		= [oz·in]


T_rms	= √(((( T_a + T_L )² × t₁ ) + ( T_L² × (t₀ - 2 × t₁ )) + (( T_a - T_L )² × t₁ )) / ( t₀ + t_s )) × (Safety Factor)
	= √ (((( + )² × ) + ( ² × ( - 2 × )) + (( - )² × )) / ( + )) ×	= [lb·in] [N·m]
		= [oz·in]

Acceleration Torque


W_T m_T	= W m (1/16) (π / 4) ρ t D² (π / 4) ρ (t ×10^-3 ) (D ×10^-3)² (1/16) ρ A B t ρ (A ×10^-3) (B ×10^-3) (t ×10^-3)
	= (1/16) (3.14 / 4) × × × ² (3.14 / 4) × × ( ×10^-3 ) × ( ×10^-3)² (1/16) × × × × × ( ×10^-3) × ( ×10^-3) × ( ×10^-3)	= [lb Kg]
W₁ m₁	= No additional load w₁ m₁ × n (1/16) (π / 4) ρ₁ h₁ D₁² n (π / 4) ρ₁ (h₁ × 10^-3 ) (D₁ × 10^-3)² n (1/16) ρ₁ A₁ B₁ h₁ n (ρ₁ (A₁ × 10^-3 ) (B₁ × 10^-3 ) (h₁ × 10^-3)) × n
	= 0 × (1/16) × (3.14 / 4) × × × ² × × (3.14 / 4) × × ( × 10^-3) × ( × 10^-3)² × (1/16) × × × × × × × ( × 10^-3) × ( × 10^-3) × ( × 10^-3) ×	= [lb Kg]
T_L	= ( W_T + W₁) µ 9.8 ( m_T + m₁) µ (l × 10^-3) (1 / (η × 0.01)) ( W₁ /2 ) r ( 9.8 m₁ /2) (r × 10^-3) (1 / (η × 0.01)) ( D_p1 / D_p2 )
	= 9.8 × ( + ) × × ( × 10^-3) × (1 / ( × 0.01)) ( / 2 ) × ( 9.8 × / 2) × ( × 10^-3) × (1 / ( × 0.01)) × ( / )	= [lb·in] [N·m]
		= [oz·in]


Δθ	= Δθ Δl ( 360° / π D ) Δl ( 360° / 2 π r ) ( D_p2 / D_p1 )
	= × ( 360 / (3.14 × ) ) × ( 360 / (2 × 3.14 × ) ) × ( / )	= [deg]

Other requirement(s)

- end of the report -

Unit Conversion

Length:

Mass:

Weight:

Inertia:

Torque:

Speed:

^°

° = For Stepper Motors input Step Angle

Friction coefficient table (reference)
Materials		Dry	Lubricated
Aluminum	Aluminum	1.0	0.3
Aluminum	Steel	0.6
Brass	Steel	0.5
Graphite	Steel	0.1	0.1
Polythene	Steel	0.2	0.2
Polystyrene	Steel	0.3	0.3
Rubber	Steel	0.4
Steel	Steel	0.8	0.2
Teflon	Steel	0.04	0.04
Wood	Wood	0.5	0.2

Positioning operation
Step 1 :	Leave the rotor inertia Jo and the gear ratio i blank if you have not selected any motor (or geared motor) yet. Then, fill in the rest of the form. The software will temporary calculate the acceleration torque with a load/rotor inertia ratio of 5:1.
Step 2 :	Select a product based on the required torque and the required speed. Then, confirm the inertia ratio to be within the recommendation. (See the motor selection tips that will appear on the result window for the detail)
Step 3 :	Return to the form and enter the rotor inertia Jo and the gear ratio i of the product you have selected to calculate the torque requirement using that particular product. If you selected a round shaft type motor (without gearhead), leave i blank or enter 1.
Rotor inertia Jo :	This value is found in the specification tables for stepping motor products.
Gear ratio i :	This value is the gear ratio of the geared motor product you selected. * These values are only used to calculate a more accurate acceleration torque.